しばらく先のことになりますが、 引退後の居住先について考え始めています。
現在は同居の子供がおりフルタイムで仕事をしているため、 通勤しやすい場所に4LDKの物件を借りていますが、 子供が独立して老後資金の目処がたった時点で、 より小さな物件に転居することを想定しています。 その後もスイスにとどまるか、 欧州の近隣諸国や日本に移るかは未定です。
その時点で物件を現金で購入できるだけの資金が手元にあるという想定で、 購入と賃借の金融上の得失を比較してみました。
関係式の導出
購入費用
記号を次のように定める。
| 項目 | 記号 |
|---|---|
| 想定運用利率 | $r$ |
| 入居年数 | $N$ |
| 物件購入価格(諸費用含む) | $P(0)$ |
| 物件売却価格(手数料控除後) | $P(n)$ |
| 毎年の支出(管理手数料、固定資産税、修繕積立金、備品修理費用など) | $c$ |
| 入居時に必要な資金 | $F_0$ |
入居時点で支払いが必要な金額は $P(0)$ だが、 購入後は毎年の支出が発生するため、 予めこの費用分も手当しておく必要がある。
計算を簡単にするためこの支出は毎年一定額 $c$ で、 入居直後に一回目の支払い、 その後は一年ごとに支払いを行うものとする。 $n$ 年後に発生する支払いを現在価値に割り引くと $ c (1+r)^{-n}$ となるため、 入居時に用意しておくべき資金 $F_0$ は下記のようになる [1]。
賃借費用
次に、 初期資金 $F_0$ を用意した状況で物件を賃借した場合の資産推移を求める。 賃貸物件では毎月の家賃に加えて更新手数料、保証料などの支払いが必要になることがあるが、 これらも全て按分して家賃に含めることとする。
| 項目 | 記号 |
|---|---|
| 入居時手数料(敷金・不動産仲介手数料など) | $c_0$ |
| 年間家賃(管理手数料、更新手数料、保証料などを含む) | $R$ |
| $n$ 年後の手持ち資金 | $F(n)$ |
計算を簡単にするため、 年間家賃は入居直後に一回目の支払いを行い、 その後は一年ごとに支払いを行うものとする。 $N$ 年後に退去する場合、 最後の支払いは入居後 $N-1$ 年時点となる。
入居後に入居時手数料と年間家賃を支払うため、 入居直後の手持ち資金 $F(0)$ は次の通り。
この資金を一年間運用すると $(1+r) F(0)$ となり、 そこから翌年の家賃 $R$ を支払うので、 一年後の手持ち資金は $F(1) = (1+r) F(0) - R$ となる。 これが毎年繰り返されるため、 1年目以降の手持ち資金は次で与えられる。
費用は前払いのため、 $N$ 年後の退去時には費用支払いが発生しないことに注意。 また退去時には敷金が返還されるが、 計算を簡単にするため今回は完全償却されるものとする。
$ n < N $ の場合の漸化式を解く。 特性方程式 $\alpha = (1+r) \alpha - R$ から $\alpha = r^{-1} R$ となるので、 漸化式は次のように変形できる。
$ n = N $ の場合に代入する。
これを家賃 $R$ について解くと次の通り。
均衡家賃
物件を購入して $N$ 年後に $P(N)$ で売却した場合、 $N$ 年後の手持ち資金は売却金額の $P(N)$ である。 一方で物件を賃借して $N$ 年後に退去した場合、 退去時点での手持ち資金は $F(N)$ である。
最初に資金 $F_0$ を用意し、 $N$ 年後に同額の手持ち資金が残れば物件の購入・賃借は経済的に得失なしといえる。 この場合の家賃を均衡家賃 $R_{eq}$ と呼ぶことにすると、 $R_{eq}$ は上で求めた家賃 $R$ で $P(N) = F(N)$ となる場合に相当する。
| 項目 | 記号 |
|---|---|
| 想定運用利率 | $r$ |
| 入居年数 | $N$ |
| 物件購入価格(諸費用含む) | $P(0)$ |
| 物件売却価格(手数料控除後) | $P(N)$ |
| 毎年の支出(管理手数料、固定資産税、修繕積立金、備品修理費用など) | $c$ |
| 入居時手数料(敷金・不動産仲介手数料など) | $c_0$ |
マンション価格を固定した場合の解析
事例: 3700万円のマンションを購入し、15年間居住
3700万円の中古マンションを購入し、 15年居住後に売却して老人ホーム等に移るケースを考える。 諸費用(仲介手数料、登記費用など)として300万円、 固定資産税、修繕積立金、管理費などの費用を年間60万円、 資産運用利率(税引き後)を年利4%と仮定すると、 入居時必要費用 $F_0$ は約4690万円となる。
購入後は年間2.5%の割合でマンションの価格が下がっていくとすると、 15年後のマンションの価値は約2530万円となる。 物件売却によって手にする金額 $P(N)|_{N=15}$ は、 さらにこれから仲介手数料を差し引いて約2450万円となる。
前節の式に代入すると均衡家賃 $R_{eq}$ は約280万円/年。 2年に1度更新手数料などが発生することを想定すると、 入居時手数料45万円、家賃+管理費が月22万5千円程度であれば、 15年後の退去時に売却価格と同額の2450万円の資産が手元に残ることになる。
なお運用利率 $r$ を保守的に2%程度と見積もると、 均衡家賃 $R_{eq}$ は月18万円程度に下がる。
単純に購入時のマンション価格+諸費用 $P(0)$ と売却価格 $P(N)|_{N=15}$ の差を15年間で按分すると約8万3千円/月となるが、 これは手元金融資産の運用益(機会損失)を考慮に入れていないため。 賃借と購入・売却を比較する際には、 この数字は用いるべきではない。
解析
物件を選択すると、 当初価格 $P(0)$、毎年の支出 $c$、入居時手数料 $c_0$ は固定される。 売却時の最終的な収入額 $P(N)$ に関しては不動産市況に左右されるが、 不動産市況が安定的で毎年一定の割合で不動産価格が下落していくと仮定すると、 この価格も定数として扱える。
均衡家賃 $R_{eq}$ を構成する残りの変数、 想定運用利率 $r$ と入居年数 $N$ が与える影響を見る。
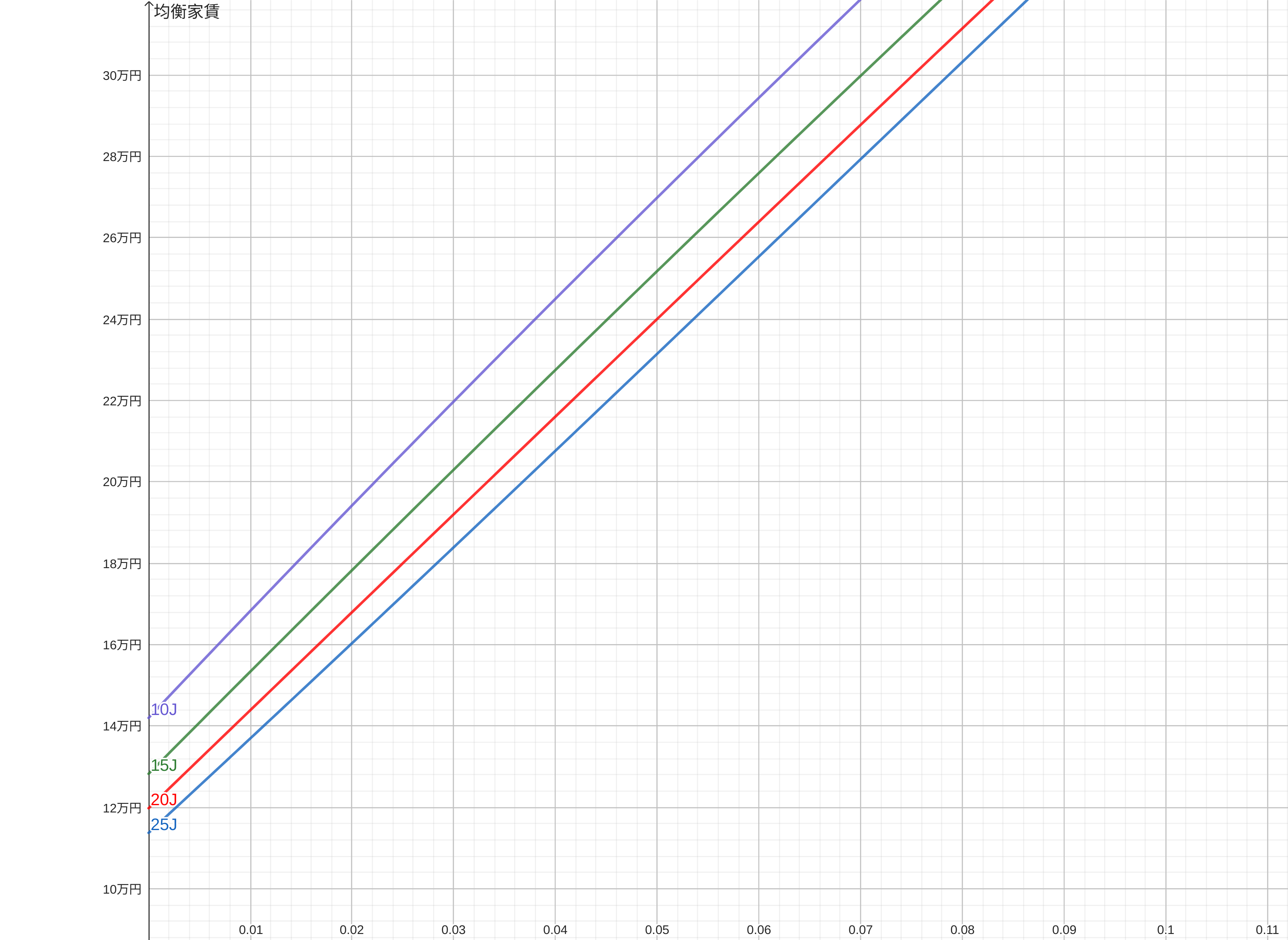 均衡家賃
均衡家賃縦軸が均衡家賃(月額、更新料は2年毎に家賃1ヶ月と仮定)、 横軸が金融資産の運用利率(年)。 10Jとコメントが付いているグラフ(紫)が入居期間10年で売却するケース、 他に15年、20年、25年のグラフを併記。
運用利率 $r$ の与える影響
運用利率 $r$ が高まると、 手元資金を運用して得られる金額が多くなるため、 均衡家賃 $R_{eq}$ は高くなる。
15年間入居時
| 運用利率 | 均衡家賃(r=0相対) |
|---|---|
| 0% | 100% |
| 1% | 120% |
| 2% | 139% |
| 3% | 158% |
| 4% | 173% |
| 5% | 196% |
運用利率が1%上がると、 家賃として支出できる金額が約20%ずつ増えていく [2]。
入居期間 $N$ の与える影響
入居期間 $N$ が短くなると総費用に占めるマンション購入・売却時の手数料の割合が上がるため、 均衡家賃 $R_{eq}$ も高くなる。
運用利率 $r$ が 4% のとき
| 入居年数 | 均衡家賃 (N=15相対) |
|---|---|
| 5年 | 124% |
| 10年 | 108% |
| 15年 | 100% |
| 20年 | 95% |
| 25年 | 91% |
マンションを購入して15年後に売却する場合と比較して、 5年しか入居せずに売却すると約2割負担が重くなり、 逆に25年入居した場合には約1割負担が軽くなる。
運用利率 $r$ が高くなると居住年数の違いによる均衡家賃への影響はやや低下するが、 短期で売却すると負担が重くなり、 長期間居住すると負担が軽くなる傾向は変わらない。
その他の考慮事項
売却時の不動産市況により物件売却価格は上下する可能性がある。 物件価格の下落が緩やかだった場合には想定よりも多額の金額が手元に残る一方で、 地震などにより不動産価値が毀損するリスクも負う。 また賃借と比べると売買には時間と手間がかかり、 特に判断力が落ちる老後に行うにはリスクが有る。
また今回の計算では考慮しなかったが、 修繕積立金の値上がりやインフレ、 税制なども最終的な得失に大きな影響を与える。
暫定的な結論
入居期間15年(たとえば60歳で早期退職し75歳まで入居)という想定だと、 購入・売却時の手数料が割高になるため、 おそらく物件を賃借したほうが経済的には得になる。
子育てを始める時点で購入する場合は、 長期入居が見込める上、 住宅ローン減税などの恩恵も受けられるため購入するメリットも大きい。
いずれにせよ実際に購入・賃借を検討するタイミングで、 その時点での税制や景況等をふまえて再検討が必要。