いずれ資産を積み上げる現役時代から貯蓄を切り崩して生活するリタイア生活への移行することになるが、 その際に必要となる資金について検討を行った。 具体的には、いつリタイアを決断するべきか、 リタイア後の資産運用指針と取り崩し計画を策定する上での指針を導いた。
関係式の導出
問題を簡単にするため、退職後には労働所得がなく、年金受給開始後には年金で生活費を賄えるものと仮定する。 この場合、貯蓄した資産で退職から年金生活開始までの生活費を支払い、年金受給開始後に必要となる一時金(たとえば老人ホーム入居費用など)が残れば良い。
記号を次のように定める。
| 項目 | 記号 |
|---|---|
| 退職時資産額 | $x_0$ |
| 退職後 $n$ 年目資産額 | $x_n$ |
| 年間引出額 | $a$ |
| 引出年数 | $N$ |
| 運用利率(インフレ調整後) | $r$ |
毎年年初に一定額 $a$ を引き出すこととすると、 第 $n-1$ 年の資産額 $x_{n-1}$ と翌年の資産額 $x_n$ には次の関係がある。
$$x_n = (x_{n-1} - a)(1+r) \quad (1)$$
$r = 0$ の場合は単純な等差数列なので
$$x_n = x_0 - aN$$
となる。
$r\neq0$ の場合には、(1) の漸化式に対して特性方程式を立てて解く。
これより (1) は次のように変形できる。
(2) を代入して、
したがって年間引出額 $a$ は次式で与えられる [1]。
$$ a = \frac{1}{1+r}\frac{r}{1-(1+r)^{-N}} x_0 - \frac{1}{1+r}\frac{r}{(1+r)^N - 1} x_N \quad (3) $$
また、この式を退職時資産額 $x_0$ について解くと次のようになる [2]。
$$ x_0 = (1 + r)\frac{1 - (1+r)^{-N}}{r} a + {(1+r)^{-N}} x_N \quad (4) $$
これは必要な年間引出額 $a$ と年金受給開始時の最終年度資産額 $x_N$ を確定させた場合に、退職するために必要となる目標貯蓄額を示している。
年金引出額が既知の場合の分析
退職に必要な資産額
年間引出額 $a$、退職金支給開始までの年数 $N$、ならびに最終年度(年金受給開始時)残余資産額 $x_N$ が決まっている場合、退職時資産額、すなわち退職に必要となる貯蓄額がどのように決まるかを分析する。これは、どの時点で引退を決断するかの指針となる。
まず (4) より退職時資産額は次式で与えられる。
$$ x_0 = (1 + r)\frac{1 - (1+r)^{-N}}{r} a + {(1+r)^{-N}} x_N $$
最終年度資産額が退職時資産額に与える影響
退職時必要貯蓄額 $x_0$ のうち、最終年度(年金受給開始時)残余資産額 $x_N$ 変動時の影響は $$\frac{\partial x_0}{\partial x_N} = (1+r)^{-N} $$ である。
これは単純な複利計算で、初年度に上記の金額だけ用意しておけば、それを毎年 $r$ の想定利率で運用することで最終年度に $x_N$ の資産額が得られることを示している。
この最終年度資産額が未達となった場合、それ以降の人生で挽回することは極めて難しいため、この部分に関しては保守的な運用が必要となる。
年間引出額が退職時資産額に与える影響
退職時必要貯蓄額 $x_0$ のうち、年間引出額 $a$ 変動時の影響は次の通り。
$$ \frac{\partial x_0}{\partial a} = (1 + r)\frac{1 - (1+r)^{-N}}{r} $$
運用利率 $r$ が高くなるほど必要貯蓄額が下がり、引出年数が長くなるほど運用利率 $r$ の影響が大きくなる。 目標とする年間引出額 $a$ を得るために必要となる貯蓄額と運用利率 $r$ の関係を図に示すと、次のようになる。
横軸が運用利率、縦軸が年間引出額 $a$ の何倍の貯蓄が必要かを表している。
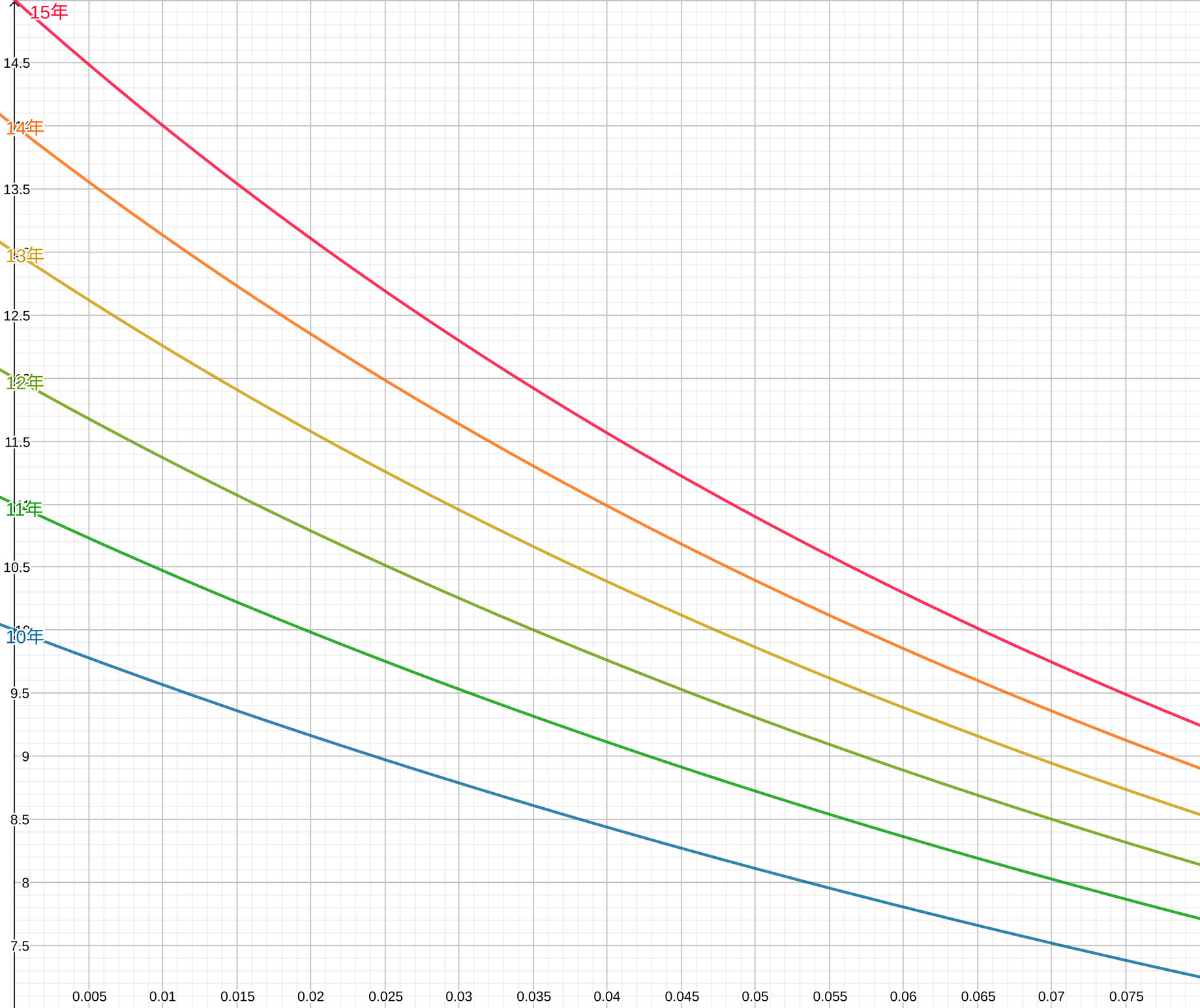
たとえば退職後10年間かけて資産を引き出す場合のグラフは、上記の青線となる。
運用利率 $r$ が 0% であれば年間引出額 $a$ の10倍の初期資産が必要となるが、運用利率が上がるに従い必要な初期資産額が減少し、運用利率2% で約9.2年分、運用利率4%で約8.4年分の初期資産があれば良いことになる。 この運用利率を高く見積もりすぎると退職後に収入が不足するリスクがあるが、一方で保守的に見積もりすぎると退職が遅れ、人生で自由に使える時間が減るという別のリスクを負うことになる。
このリスクを軽減するには、次のような方法が考えられる。
まずは「必要金額」と「節約できる費用」を分けて考え、 保守的な運用利率で前者を賄えるようにしつつ、 運用状況に応じて「節約できる費用」への支出額を増減する方法。
なお、この「必要金額」は最低限度の生活費ではなく、最低限実現したいと思う娯楽費用なども含めて考える。 たとえば旅行には毎年一度は行きたいということであれば、その旅行費用は「必要金額」に含める。 一方で滞在先のホテルのグレードを上げる、旅行の回数を増やすといったことは「節約できる費用」として取り扱う。
次に完全にリタイアするのではなく、パートタイム労働などで収入を一部維持する方法。 運用利率が目標を達成しなかった場合には、労働収入を増やすことで収入を調整する。
資産額を固定した場合の分析
年間引出額に対する資産額の影響
運用が想定よりも好調で初期資産が増えた、 もしくは最終年度に必要と想定していた金額の増減があった場合に、どのような影響が出るかを見る。(3) より年間引出額は次で与えられる。
$$ a = \frac{1}{1+r}\frac{r}{1-(1+r)^{-N}} x_0 - \frac{1}{1+r}\frac{r}{(1+r)^N - 1} x_N $$
退職時資産額 $x_0$ と最終年度資産額 $x_N$が変化した際に、どのように年間引出額に影響を与えるかを考える。
初期資産額の与える影響
年間引出額 $a$ のうち、退職時資産額 $x_0$ 変動時の影響は次の通り。
$$ \frac{\partial a}{\partial x_0} = \frac{1}{1+r}\frac{r}{1-(1+r)^{-N}} $$
運用利率 $r$ が 0% の場合には、年間引出額は退職時資産額 $x_0$ の増加分に対して単純に $\frac{x_0}{N}$ だけ増えることになる。運用利率が上がると引出額も上がり、また引出年数が増えるほど引出額に与える影響が大きくなる。
運用利率に応じた年間引出額 $a$ の変化率と運用利率 $r$ の関係を図に示すと、次のようになる(青色が引出期間10年、赤が15年、その間は1年刻み)。横軸が運用利率、縦軸が利率0%のときの年間引出額と比べて何倍の引き出しができるかを表している。
いずれも実際には曲線だが、運用期間15年、運用利率10%以下であれば一次関数で近似できる。
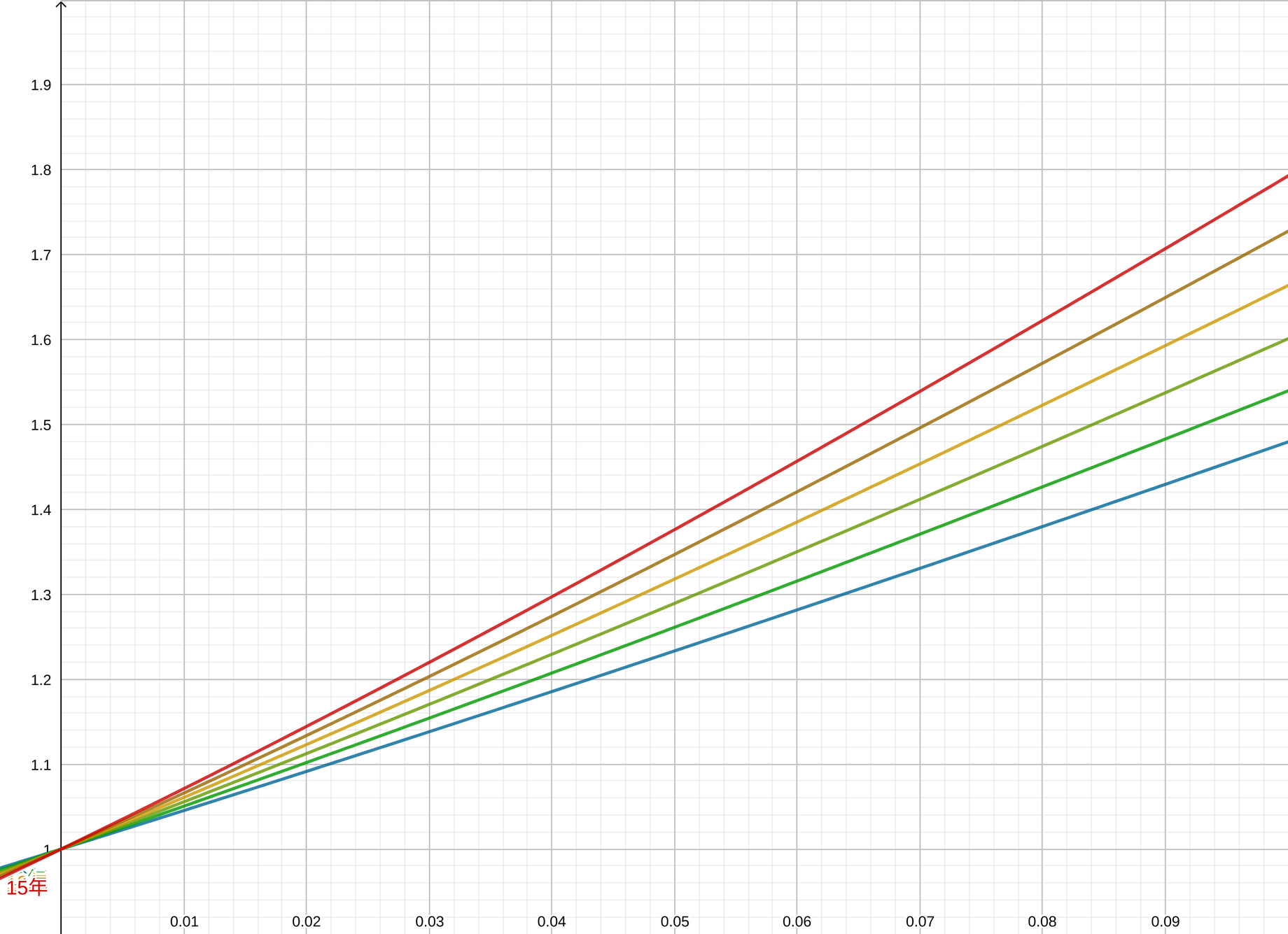
たとえば10年かけて取り崩す場合(青線)、 運用利率が0の場合には毎年の引出額は初期資産増減額の $\frac{1}{10}$ である。 具体的には初期資産が1,000万円増加すれば、10年間、毎年100万円ずつ余分に引き出せる。
運用利率1%だと年間引出額は104.5万円、2%で109.1万円、4%だと118.6万円と増加することになり、 概算として年利1%につき年間引出額が4.6%増える。 取崩し期間を15年にすると運用利率の影響はさらに大きくなり、 概算として年利1%につき年間引出額が7.4%増える。
年間引出額増加率
| 年数\利率 | 1% | 2% | 4% |
|---|---|---|---|
| 5 | 2.00% | 4.00% | 7.99% |
| 10 | 4.54% | 9.14% | 18.55% |
| 15 | 7.11% | 14.45% | 29.72% |
最終年度資産額の与える影響
年間引出額 $a$ のうち、最終年度資産額 $x_N$ 変動時の影響は次の通り。
$$ \frac{\partial a}{\partial x_N} = -\frac{1}{1+r}\frac{r}{(1+r)^N-1} $$
運用利率 $r$ が 0% の場合には、年間引出額 $a$ は最終年度資産額 $x_N$ に対して単純に $\frac{x_N}{N}$ だけ減ることになる。 運用利率が上がると引出額への影響は小さくなり、また引出年数が増えるほど運用利率 $r$ が引出額を減少させる割合が大きくなる。
運用利率に応じた年間引出額 $a$ の変化率と運用利率 $r$ の関係を図に示すと、次のようになる(青色が引出期間10年、赤が15年、その間は1年刻み)。 横軸が運用利率、縦軸が利率0のときの年間引出額減少幅と比べて、どれだけ減少幅が変化したかを示している。
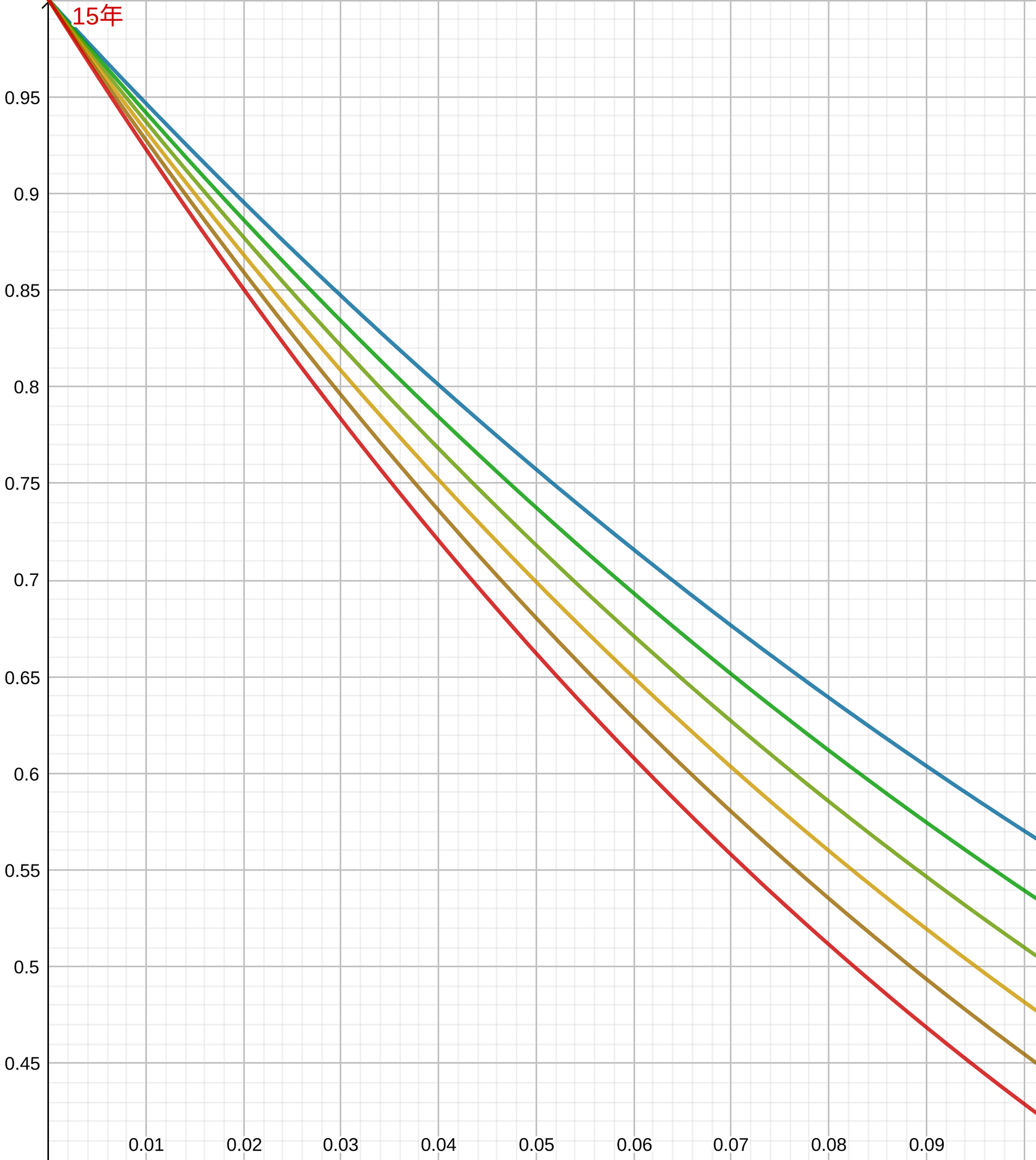
たとえば10年かけて取り崩す場合、運用利率が0%の場合には毎年の引出額は最終年度資産額の10%減少する。最終年度資産額として1,000万円多く残すためには、10年間、毎年100万円ずつ引出額を減らす必要がある。
運用利率が上がるに従い、引出額に与える影響は非線形的に小さくなる。具体的には運用利率1%だと年間引出額の減少額は95.6万円、2%で91.3万円、4%だと83.3万円の減少にとどまる。
年間引出額減少率
| 年数\利率 | 1% | 2% | 4% |
|---|---|---|---|
| 5 | 98.02% | 96.08% | 92.31% |
| 10 | 95.58% | 91.33% | 83.29% |
| 15 | 93.19% | 86.74% | 64.44% |
今後の課題
今回はリスクに関する分析を行っていないため、運用利率が想定を下回った場合にどのような影響が出るのか、その可能性はどの程度かを明らかにする必要がある。 また引退後に想定以上の運用利益もしくは損失が出た場合に、 翌年以降の支出額をどのように調整するかの指針を定めておくことが望ましい。
加えて実質的な運用利率や所得に影響を与える税制、 医療・介護制度(公的保険、医療費負担、介護施設など)、 日本・スイス間の社会保障協定についても調査が必要。
参考
関連分野
年金財政における計量的管理・運営を行う数学的手法(年金企業連合会)として、年金数理がある。個人の年金収支ではなく年金基金の運営上の課題を解決することが主目的だが、使用する数学などは参考になると思われる。
またファイナンシャルプランナー資格試験分野の内、ライフプラニングと資金計画、金融資産運用などが該当する。
表計算ソフト
表計算ソフトは、年金の計算に必要となる関数を実装している。
年金現価係数
元金を一定利率 $r$ で複利運用しながら毎年一定金額を取り崩していくとき、現在いくらの元本で複利運用を開始すればいいかを求める際の係数。
$$PV = \frac{1-(1+r)^{-n}}{r}$$
資本回収係数
元金を複利運用しながら一定期間 $n$ で取り崩す場合の毎年の受取額を求める際の係数。開始時点で取り崩さず1年間運用し、それから取り崩すことを想定している。(4) の式では年初に取り崩してから運用することを想定しているため $(1+r)$ 倍の差が出ている。
$$PMT = \frac{r}{1-(1+r)^n}$$